Le processeur
Dans le chapitre précédent, nous avons assemblé des portes logiques pour créer un circuit capable d'additionner deux nombres binaires. C'est déjà pas mal, mais si nous sommes honnêtes un instant, notre circuit actuel est assez limité comparé à un ordinateur.
Imaginez que vous ayez construit ce circuit additionneur. Si vous voulez calculer 5 + 3, vous envoyez les signaux correspondants (101₍₂₎ et 11₍₂₎) et le circuit calcul le résultat. Mais si, tout à coup, vous avez besoin de faire une soustraction, ou de vérifier si deux nombres sont égaux ? Votre circuit d'addition ne suffit plus. Vous devez débrancher vos fils et vos transistors et reconstruire un circuit de soustraction ou de comparaison.
C'est le problème qu’avait les premiers calculateurs électroniques (comme l'ENIAC au début des années 40 que nous avons évoqué précédemment, cf. chapitre 1) : pour changer de programme, il fallait physiquement recâbler la machine. Notre objectif dans ce chapitre est donc de transformer notre circuit, jusque-là statique, en une machine polyvalente.
La première étape consiste à créer tous les circuits dont nous allons avoir besoin pour nos différentes opérations, côte à côte, par exemple :
- Un circuit d'addition (comme celui du chapitre 3).
- Un circuit de soustraction.
- Un circuit pour l'opération logique ET (AND).
- Un circuit pour l'opération logique OU (OR).
Nous utiliserons 2 entrés, nommés A et B, de 8 bits chacune, c’est-à-dire 8 symboles binaires (imaginez une gaine dans laquelle il y aurai 8 fils). Nous allons les connecter à tous nos circuits en même temps. Le problème est alors que nous nous retrouvons en permanence avec quatre résultats différents simultanément en sortie. Par exemple, si A=00000101₍₂₎ (5 en décimal) et B=00000011₍₂₎ (3 en décimal), le circuit d'addition renvois « 00001000₍₂₎ » (8 en décimal), le circuit de soustraction renvois en même temps « 00000010₍₂₎ » (2 en décimal), etc. Il nous faut un moyen d’ignorer les sorties qui ne nous intéressent pas et de n'en sélectionner qu'une seule : l’opération désirée à ce moment-là.
Pour résoudre ce problème, nous avons besoin d'un nouveau composant : un Multiplexeur.
Voyez le multiplexeur comme un aiguillage de chemin de fer. Plusieurs circuits arrivent (les résultats de nos opérations), mais un seul repart vers la sortie à la fois.
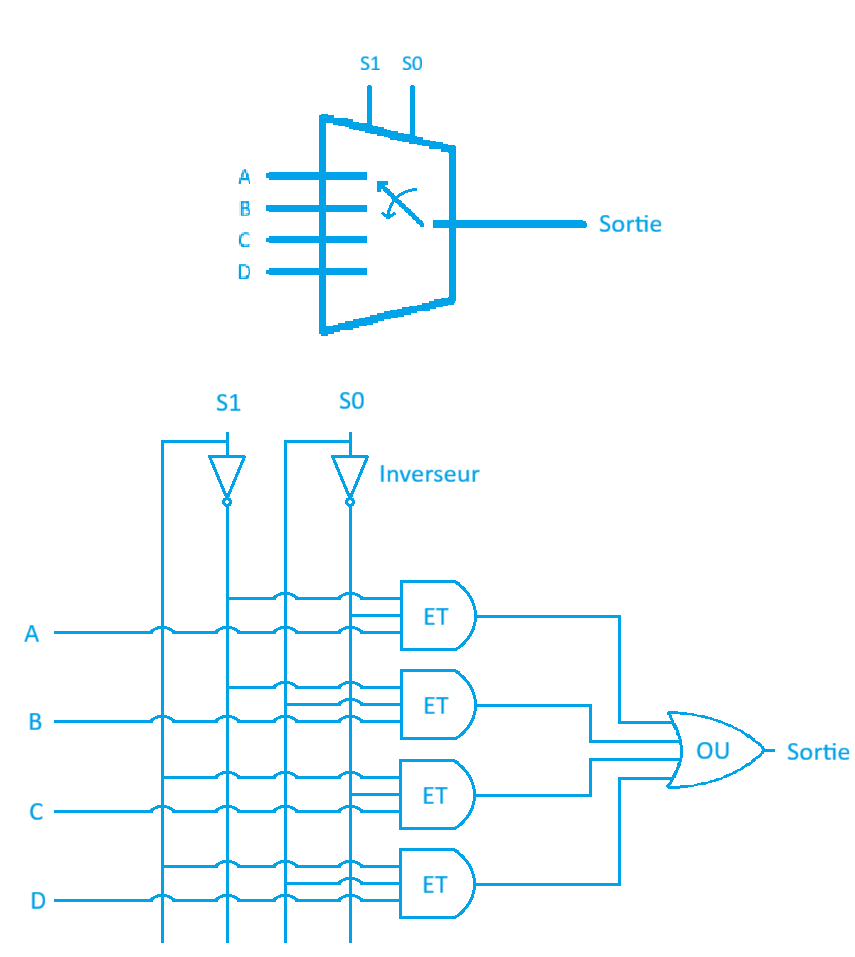 Schéma simplifié d'un multiplexeur
Schéma simplifié d'un multiplexeurComme vous pouvez le voir sur le schéma logique ci-dessus, en plus des quatre entrés réservés à nos opérations possibles (Addition, Soustraction, ET et OU), le multiplexeur à deux entrées spéciales appelées « lignes de sélection » (S0 et S1), car les 2 bits (2 symboles binaires) nous permettent de réaliser 4 combinaisons différentes pour choisir la sortie que nous désirons : 00₍₂₎, 01₍₂₎, 10₍₂₎, et 11₍₂₎.
C'est ici que se produit la magie conceptuelle de l'informatique. Jusqu'à présent, le binaire représentait des données (des nombres). Ici, il représente une instruction que l’on donne au multiplexeur. Par exemple, si on envoi le code S0 = 0₍₂₎ et S1 = 0₍₂₎ au multiplexeur, il sélectionne la sortie de l'additionneur. Si on envoi le code S0 = 0₍₂₎ et S1 = 1₍₂₎, il sélectionne la soustraction, etc. Nous appelons ce code que nous envoyons sur les lignes de sélection un « Opcode » (Code Opération), car il n’est pas un simple nombre, il est une instruction donnée au multiplexeur.
Grâce à cet assemblage de circuits via notre multiplexeur, nous venons de créer une « Unité Arithmétique et Logique » (abrégée ALU en anglais). Ce circuit sert de calculatrice dans un ordinateur et est capable en plus d’effectuer certaines opérations logiques (ex. comparaison). Il prend deux nombres en entrée, et un Opcode pour savoir quoi en faire. Cependant, elle à un défaut majeur : elle n'a aucune mémoire. Imaginons l’exemple suivant : nous voulons réaliser l’addition 256 + 128. Notre ALU possède 8 entrés, or, le nombre 256 nécessite 9 bits pour être écrit en binaire : 100000000₍₂₎. Il est donc impossible de réaliser cette opération sur notre ALU. Une solution simple serait juste d’agrandir le circuit afin d’avoir des entrés avec plus de bits, mais cela ne ferait que repousser le problème. Pour le résoudre définitivement, il n’y a qu’une solution : décomposer le calcul en nombres plus petits : 128 + 128 + 128. Le résultat sera identique, mais cette fois ci, nous avons 3 nombres codés sur 8 bits, notre ALU peut donc travailler avec. Or, pour faire ce calcul, il faut d'abord calculer 128 + 128, noter le résultat quelque part, puis l'utiliser pour l'addition suivante, puisque nous n’avons que 2 entrés (A et B).
Il nous faut une mémoire très rapide (pour ne pas ralentir nos calculs), faite de transistors. Vous pourriez penser à la mémoire Flash (avec la grille flottante) que nous avions vu au chapitre 2, mais en pratique, elle est trop lente pour un processeur. Nous allons à la place créer un circuit qui boucle pour stocker chaque bit (0 ou un 1). On appelle ce montage une Bascule (ou Latch / Flip-Flop). Nous n’allons pas rentrer en détail ici dans sa conception car l’intérêt est très limité, son comportement est le même que la mémoire Flash que nous avons déjà vu mais en beaucoup plus réactif. Pour tout de même avoir une intuition de son fonctionnement, vous pouvez imaginer une porte logique dont la sortie est reconnectée à sa propre entrée. Le signal « tourne en rond » et s'auto-entretient tant qu’on ne le libère pas. Il est donc capable de mémoriser un état (0 ou 1) indéfiniment tant qu'il est alimenté.
Nous allons aligner 8 bascules (Flip-Flop) côte à côte afin de pouvoir mémoriser un nombre de 8 bits, le résultat de notre ALU. Cet assemblage s'appelle un « Registre ». Les registres sont la mémoire de travail ultra-rapide du processeur. Ils servent de « brouillon » ou mémoire temporaire. Dans les processeurs modernes, il y a en général plusieurs centaines de registres (cela dépend du nombre de circuits différents qui ont besoin de stocker temporairement des choses). Ils ont tous un nom technique tel que « EAX », « EBX », « ECX », « ESP », « EBP », etc. Cependant, pour faciliter les choses et nous permettre de retenir à quoi ils servent, certain d’entre eux on un nom plus simple qui décrit leur fonctionnalité. C’est le cas du registre utilisé par notre ALU. On l'appelle « l'Accumulateur ». Il est branché directement à l’entrée et à la sortie de notre ALU pour recueillir le résultat du calcul en cours, prêt à être réutilisé pour le calcul suivant.
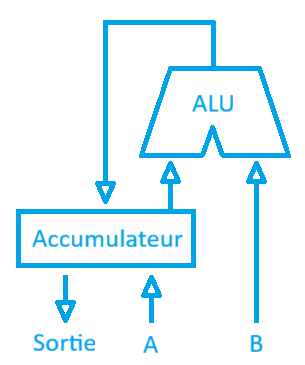 Schéma d'une microarchitecture à accumulateur
Schéma d'une microarchitecture à accumulateurBien que ce schéma semble fonctionnel en théorie, en pratique, il n’est pas viable. Regardez notre circuit : le registre accumulateur envoie des données dans l'ALU -> elle calcule -> le résultat retourne dans le registre. C'est une boucle. L'électricité se déplaçant presque à la vitesse de la lumière, sans contrôle, les données tourneraient en boucle à une vitesse folle, devenant instables et chaotiques. Pour éviter cela, il nous faut un chef d’orchestre, un métronome. Quelqu'un qui dise : « Tout le monde fige sa position... On calcule... On écrit le résultat... Et on recommence. »
Pour régler ce souci, on introduit un nouveau composant physique : un cristal de quartz. C’est un minéral piézoélectrique, qui, lorsqu'il est stimulé par l'électricité, vibre à une fréquence extrêmement précise. Imaginez qu’on fusionne cela avec un transistor, on obtient alors une sorte d’interrupteur qui, lorsqu’il est alimenté s’ouvre et se ferme en boule à l’infini. La vibration du matériau est alors utilisée pour générer une alternance régulière de 0 et de 1 (on appelle cela un signal carré). Ce composant s'appelle une « horloge » (clock en anglais). Son signal va pouvoir être utilisé dans tous nos circuits afin de les cadencer ensemble, pour s’assurer que les opérations soient réalisées dans l’ordre que nous désirons et au moment souhaité. En effet, jusqu’à présent, nos circuits recevaient du courant en permanence. A partir de maintenant, nous allons créer un nouveau référentiel temporel qu’on appelle un « cycle ». Voyez cela comme une unité de temps très courte. Au lieu de dire à notre circuit que nous voulons qu’il fasse l’opération pendant 1 seconde, nous allons pouvoir lui dire que nous voulons qu’il la fasse pendant 1 cycle (un couple 1 et 0 produit par l’horloge, une vibration du cristal).
- TIC (signal 1) : le registre s'ouvre. L'ALU a le droit de travailler. Le circuit renvoi le résultat du calcul.
- TAC (signal 0) : Le résultat est figé et sauvegardé dans le registre.
La vitesse à laquelle l’horloge vibre est ce qu'on appelle sa fréquence, mesurée en Hertz (Hz). Un processeur moderne à par exemple une fréquence de 3 GHz (Gigahertz), ce qui veut dire qu’il contient une horloge qui bat la mesure 3 milliards de fois par seconde. À chaque battement un nouveau cycle, une opération élémentaire est effectuée. La durée d’un cycle dépend donc de la fréquence de l’horloge, chaque processeur peut avoir des cycles d’une durée différente, plus ils sont court, plus le processeur est rapide (mais ce n’est pas le seul facteur qui rentre en jeu pour déterminer la puissance).
Rassemblons toutes les pièces du puzzle que nous avons créées depuis le début de ce cours. Nous avons :
- L’ALU : Le circuit qui fait les calculs.
- Le Multiplexeur : Le circuit qui interprète le code binaire (Opcode) pour diriger les signaux.
- Les Registres : Le circuit pour stocker les résultats intermédiaires ou temporaires.
- L'Horloge : La puce qui bat la mesure pour synchroniser le tout.
Reliez tous ces composants entre eux dans une seule boîte et vous obtenez un processeur (CPU : Central Processing Unit, en anglais).
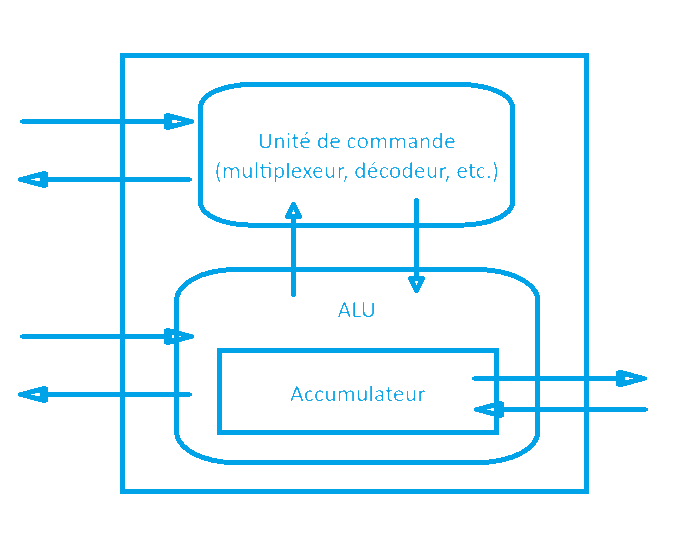 Architecture simplifiée d'un processeur
Architecture simplifiée d'un processeurVoilà ce qu'est, fondamentalement, un processeur : un circuit complexe capable de lire une instruction binaire (« 010010... »), de l'interpréter comme une action à réaliser (additionner le registre et l’entrée), d'exécuter cette action au rythme effréné d'une horloge, et de stocker le résultat. Bien entendu, les processeurs modernes savent faire un très grand nombre d’opérations différentes et comportent bien plus de circuits que ce modèle simpliste. On pourra par exemple citer « l’unité de calcul en virgule flottante » (abrégée FPU en anglais), un circuit qui permet de faire les mêmes opérations que l’ALU (en plus évolué car il supporte également les multiplications, divisions, racines carrées, etc.) mais avec des nombres à virgule.
Dans la suite de ce cours, nous allons nous pencher sur le développement informatique, c’est-à-dire, le fait d’envoyer les bonnes instructions (opcodes) au processeur de notre machine de sorte qu’elle fasse dans un ordre précis ce que l’on souhaite. Cependant, pour l'instant, notre CPU a une mémoire minuscule (quelques registres) et ne sait pas communiquer avec le reste de l’ordinateur (clavier, écran, souris, etc.) Nous verrons donc dans le prochain chapitre comment palier cela.
