Les transistors sont les composants principaux des ordinateurs modernes, qui en comportent souvent plusieurs milliards. Dans le chapitre précédent, nous avons établi qu’ils agissent comme un interrupteur contrôlé par un courant électrique. À quoi peut alors bien servir le fait d'assembler des milliards d'interrupteurs microscopiques dans un ordinateur ?

La réponse se trouve dans leur capacité à contrôler le flux d'électricité de manière binaire. Un transistor, dans son usage le plus simple, ne connaît que deux états fondamentaux : soit il laisse passer le courant (état "fermé" ou "passant"), soit il le bloque (état "ouvert" ou "bloqué"). C'est tout. Il n'y a pas d'état intermédiaire.

Cette dualité est la pierre angulaire de toute l'informatique moderne. À partir de maintenant, au lieu de voir le transistor comme un simple interrupteur, nous allons le voir comme un moyen de représenter une information. Nous allons décider, par convention, que l’état dans lequel le transistor laisse le courant passer (présence de tension) est représenté par le symbole « 1 ». L'autre état, où le courant ne passe pas (absence de tension), est représenté par le symbole « 0 ». C'est là qu'intervient le système de numération binaire. Mais qu’est-ce que c'est, au juste ?

Pour comprendre le binaire, il faut d'abord se pencher sur le fonctionnement de notre propre système de numération. En français, comme dans la plupart du monde, nous utilisons le système de numération indo-arabe pour compter. Ce système est composé de dix symboles distincts pour représenter des quantités : « 0, 1, 2, 3, 4, 5, 6, 7, 8, et 9 ». Ces symboles sont arbitraires ; ils n'ont de sens que parce que nous avons collectivement appris à les associer à une quantité. Ils sont d’ailleurs différents dans d’autres langues.

Puisque nous disposons de dix symboles différents, que se passe-t-il lorsque nous souhaitons compter au-delà de neuf, le symbole de plus grande valeur dont nous disposons ? C'est simple, nous appliquons la règle suivante : nous réinitialisons notre symbole et tous ceux à sa droite à celui de départ, puis nous incrémentons d’une unité le symbole à sa gauche. C'est ainsi qu'après « 9 », nous obtenons « 10 » : le neuf est réinitialisé, et on ajoute 1 à gauche. On appelle cette façon de compter la « notation positionnelle ». Cela signifie que la valeur d'un symbole dépend de sa position dans le nombre. Par exemple, dans le nombre « 222 », chaque symbole « 2 » a une signification différente. Le « 2 » de droite représente deux unités. Celui du milieu représente deux dizaines (vingt). Celui de gauche représente deux centaines (deux cents). Chaque position vaut dix fois plus que la position à sa droite.

Dans ce système de numération, le nombre de symboles disponibles est appelé la « base ». Étant donné que le système indo-arabe possède dix symboles distincts, on dit qu'il est en base 10, c'est un système décimal. Le binaire fonctionne sur exactement le même principe, mais au lieu de dix symboles, il n'en possède que deux : « 0 » et « 1 ». C'est donc un système en base 2.

Pour compter en binaire, on commence comme en décimal avec « 0 », puis « 1 ». Arrivé à « 1 », nous avons épuisé tous nos symboles. Que faisons-nous ? Nous appliquons la même règle que pour le système décimal : nous réinitialisons la position à « 0 » et nous incrémentons la position de gauche. Ainsi, après « 1 », vient « 10 ». Ce nombre « 10 » en binaire représente la même quantité que le symbole « 2 » en décimal. Pour ne pas confondre les systèmes dans la suite de ce cours, nous utiliserons des indices (petits nombres en bas à droite entre parenthèses) pour indiquer la base avec laquelle nous comptons dès lors que nous n’utilisons pas le système décimal. Ainsi, compter en binaire de 0 à 8 s’écrira comme ceci : 0₍₂₎, 1₍₂₎, 10₍₂₎, 11₍₂₎, 100₍₂₎, 101₍₂₎, 110₍₂₎, 111₍₂₎, 1000₍₂₎. Vous remarquerez que le chiffre 4 nécessite 3 symboles pour être écrit en binaire (« 100₍₂₎ »), et le chiffre 8 en nécessite 4 (« 1000₍₂₎ »). Cela est dû au fait que nous avons moins de symboles à disposition, nous devons donc utiliser plus de positions pour contenir la même information. L’opposé est également vrai. En informatique, une autre base est très utilisée car elle est pratique pour représenter de longs nombres : l'hexadécimal, ou base 16. Elle utilise seize symboles : « 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 », puis, n'ayant plus de chiffres, on continue avec des lettres : « A, B, C, D, E, F ». Le symbole A₍₁₆₎ vaut 10 en décimal, B₍₁₆₎ vaut 11, C₍₁₆₎ vaut 12, D₍₁₆₎ vaut 13, E₍₁₆₎ vaut 14 et F₍₁₆₎ vaut 15. Si on compte en hexadécimal, après F₍₁₆₎, on applique la même règle et on obtient 10₍₁₆₎, qui vaut 16 en décimal.

Il existe une méthode simple pour convertir un nombre de n'importe quelle base en décimal. On multiplie les valeurs en décimal des symboles à toutes les positions par la base exposant la position, et on additionne le tout.

Pour illustrer cela, le tableau ci-dessous (appelé table de pondération) présente un exemple de conversion du nombre binaire 10011₍₂₎ en décimal :

Pour connaitre la valeur du symbole « 1 » le plus à gauche, on multiplie sa valeur en décimal (1 également) par 2 puisque le binaire est en base 2, exposant 4 puisqu’il est à la quatrième position. Il en va de même pour l’hexadécimal, par exemple avec le nombre DA2₍₁₆₎ :

Dans ce cas, le symbole le plus a gauche est « D » et il vaut 13 en décimal. Nous le multiplions donc par 16 puisque nous somme en base 16, puissance 2 pour la position.

Si vous avez suivi jusqu’ici, vous avez compris le principal : décimal, binaire, hexadécimal, c’est du pareil au même. La seule chose qui change, c'est le nombre de symboles disponibles. La règle de la notation positionnelle reste identique. Nous pouvons donc représenter la même information (une quantité) avec différentes notations.

Maintenant que nous avons vu cela, nous pouvons revenir à nos transistors. Comme nous l'avons dit précédemment, ils fonctionnent de manière binaire (état 0 ou 1). Nous allons maintenant nous servir du système de numération binaire pour décrire l'état de circuits électroniques.

Prenons un exemple. Réalisons un petit montage qui consiste à connecter deux transistors (A et B) en série (l'un après l'autre) à une source de courant.

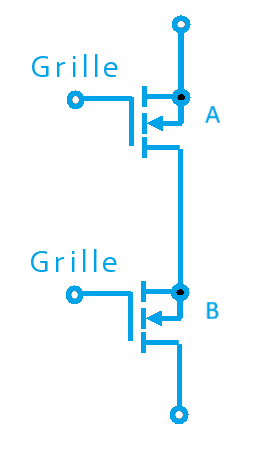
Tant qu’un courant n’est pas appliqué sur la grille des deux transistors (A=0 et B=0), les interrupteurs sont en position ouverte. Le courant ne passe pas. La sortie du circuit est à l'état 0. Si on applique une tension sur A (A=1) mais pas sur B (B=0), le premier interrupteur se ferme, mais le second reste ouvert. Le courant ne passe toujours pas jusqu’au bout du circuit (Sortie = 0). Même chose si A=0 et B=1 : Sortie = 0. Il n'y a qu'un seul cas où le courant peut traverser le circuit : lorsque A ET B sont à l'état 1. Dans ce cas, les deux interrupteurs sont fermés, donc le courant passe. La sortie passe à l'état 1.

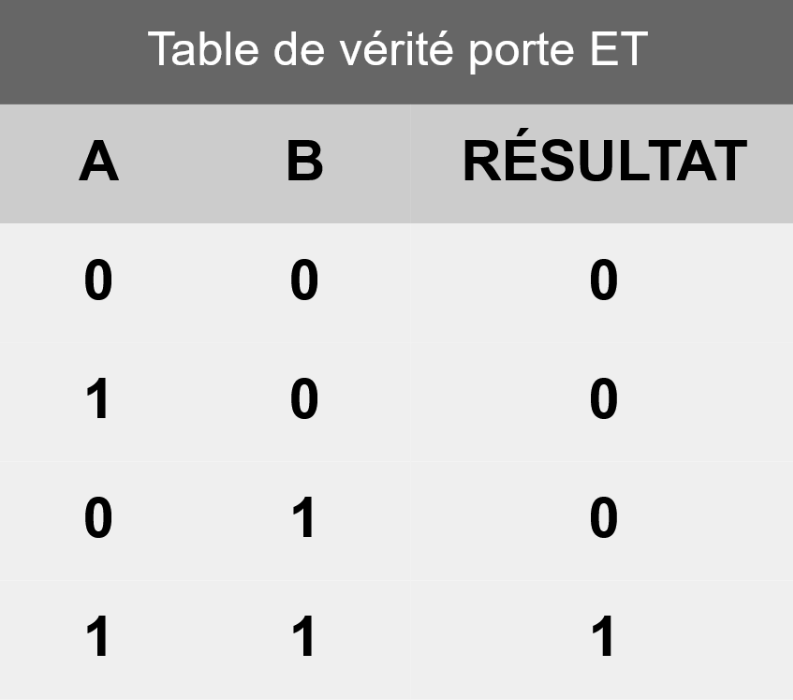
Nous venons de décrire un circuit fondamental. On l'appelle une « porte logique », et celle-ci porte le nom de porte « ET » (ou AND en anglais). On peut résumer son comportement dans un tableau appelé « table de vérité » qui le reflète :

Nous pouvons de la même manière, réaliser une autre porte logique en branchant cette fois deux transistors en parallèle (côte à côte) :

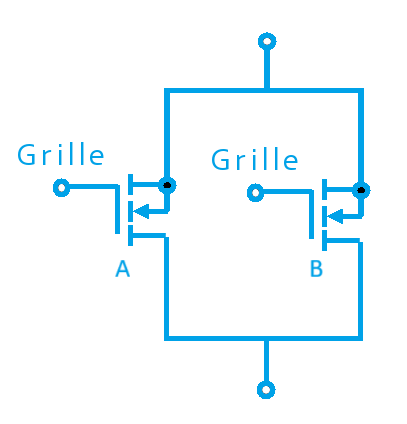
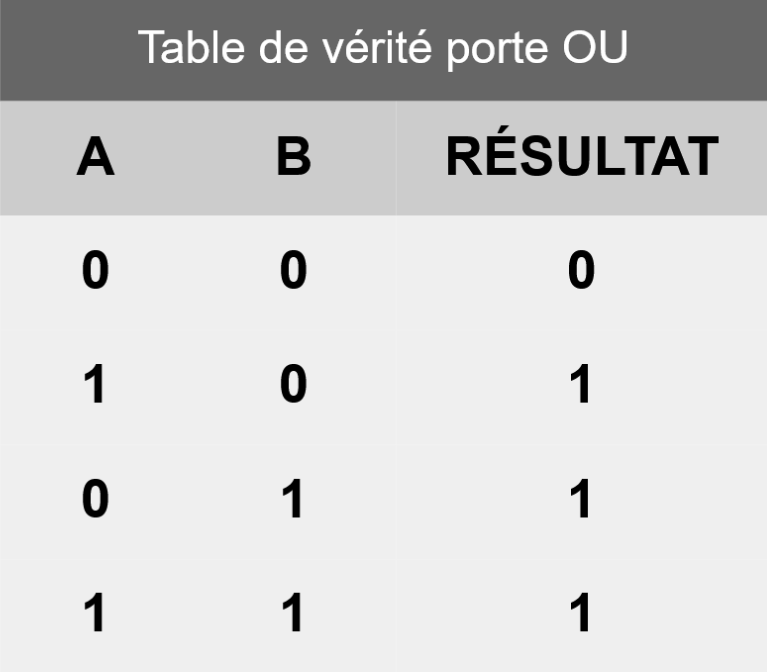
Ici, le courant peut passer dès lors qu'au moins un des deux chemins est ouvert. Si A=0 et B=0, tout est bloqué (Sortie = 0). Mais si A=1 OU B=1 (ou les deux), le courant trouve un chemin et la sortie passe à 1. C'est la porte « OU » (ou OR en anglais). Sa table de vérité est la suivante :

Il existe une troisième porte de base essentielle réalisée avec un seul transistor et une résistance dite "pull-up". Nous n’allons pas rentrer plus dans le détail de sa réalisation ici car c’est inutile pour la suite de ce cours, mais nous allons présenter son comportement. C'est un circuit où si l'entrée est 0, la sortie est 1, et si l'entrée est 1, la sortie est 0. On l’appelle la porte « NON » (NOT en anglais), ou parfois simplement « inverseur » car ça permet d’inverser l’état d’un circuit.

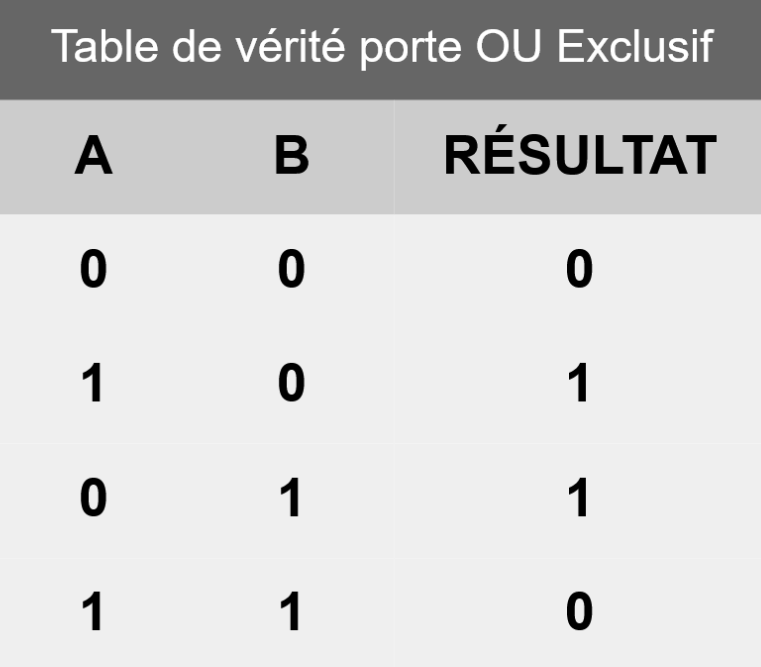
« À quoi ça sert les portes logiques ? » allez-vous me dire. Nous avons assemblé des transistors pour faire des circuits, et alors ? En réalité, l’intérêt de ces portes logiques apparaît lorsqu'on réalise que l'on peut les chaîner de sorte que la sortie d'une porte devienne l'entrée d'une autre. Pour démontrer cela, créons une porte un peu plus complexe : la porte « OU Exclusif » (ou XOR). Son comportement est le suivant : la sortie est à 1 si l'entrée A ou l'entrée B est à 1, mais pas les deux en même temps. C'est une porte "soit l'un, soit l'autre". Sa table de vérité est la suivante :

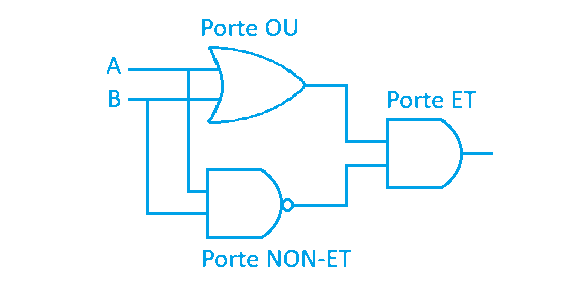
Pour la réaliser, nous pouvons repartir de notre porte « OU ». La seule différence est que quand les deux entrées sont à « 1 », la sortie doit être à « 0 ». Or, vous remarquerez que ce comportement est exactement l'inverse de celui de la porte « ET ». En effet, sa sortie est toujours à « 0 », sauf quand les deux entrées sont à « 1 ». Ainsi, si nous l'inversons, nous obtenons une porte « NON-ET » dont la sortie en combinaison avec une porte « OU » peut être utilisé comme entré d'une autre porte « ET » afin de réaliser notre porte « OU Exclusif » comme suit :

Cette porte va nous permettre de tenter de faire quelque chose d’un peu intelligent. Nous allons réaliser un circuit d’addition avec des portes logiques. Regardons tout d’abord comment se fait une addition de deux symboles binaires :

0 + 0 = 0₍₂₎

0 + 1 = 1₍₂₎

1 + 0 = 1₍₂₎

1 + 1 = 10₍₂₎

Ce dernier cas est crucial car 1 + 1 en entré ne donne pas « 1 » en sortie mais « 0 » ainsi qu’une retenue de 1 (tout comme 5 + 5 en décimal donne 0 et une retenue de 1). Pour additionner deux chiffres binaires (A et B), nous avons donc besoin de deux sorties à notre circuit : une pour le Résultat (la somme) et une pour la Retenue (le report). Écrivons maintenant la table de vérité de ce circuit que nous allons réaliser :

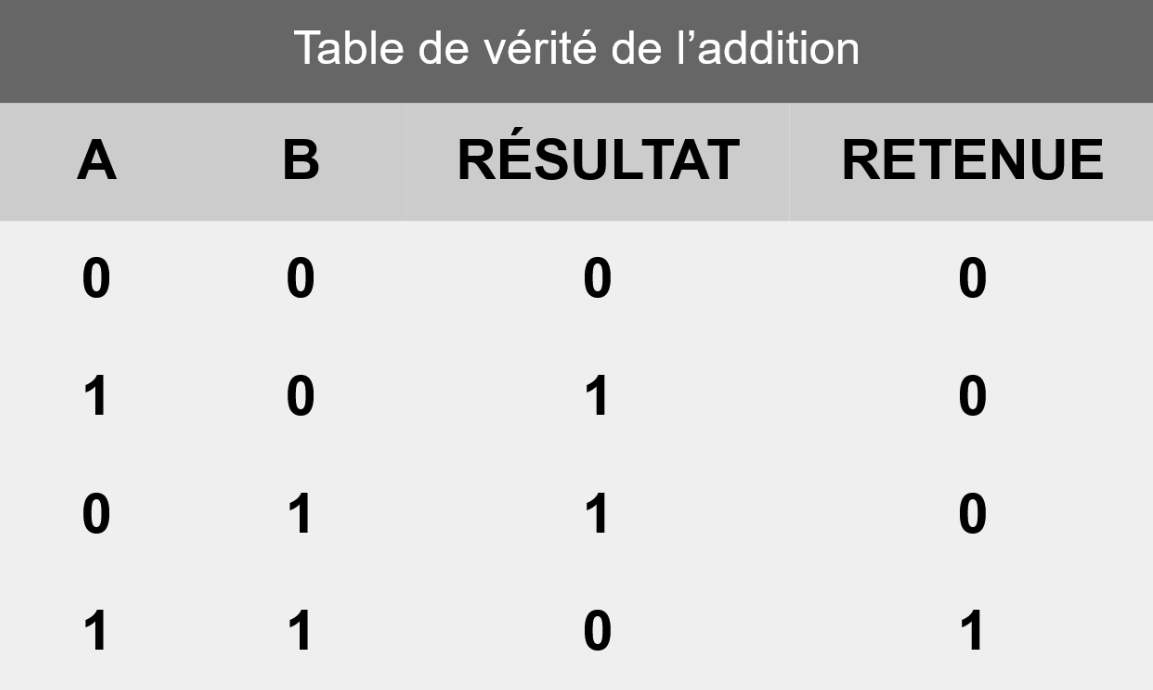
Regardez attentivement les colonnes de sortie du circuit que nous tentons de réaliser. La colonne Résultat qui contient « 0, 1, 1, 0 » ne vous rappelle rien ? C'est exactement la colonne de sortie de la table de vérité de notre porte XOR ! Et la colonne Retenue qui contient « 0, 0, 0, 1 » ? C'est exactement la colonne de sortie de la table de vérité de notre porte ET !

Le tour est joué. Pour construire un circuit électronique capable d'additionner deux chiffres binaires, il nous suffit de prendre nos deux entrées A et B et de les connecter en parallèle à une porte XOR et à une porte ET. La sortie de la porte XOR sera notre Résultat, et la sortie de la porte ET sera notre Retenue.

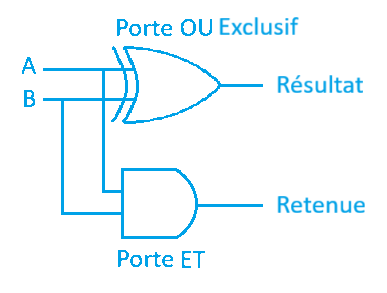
Nous venons de construire un circuit appelé « Demi-Additionneur » (Half-Adder).

Pourquoi ce nom ? La raison est que ce circuit est limité a deux entrées. Or, dans la pratique, les ordinateurs peuvent réaliser des calculs avec bien plus de symboles. Pour cela, ils utilisent des circuits avec trois entrées, ce qui leurs permet de les chainer entre eux, la troisième entrée servant a recevoir le résultat du circuit précédent, ce qui permet donc des opérations d'addition successive. Pour réaliser ce circuit avec une entrée supplémentaire, nous devons ajouter une porte ET, OU Exclusif et OU supplémentaire :

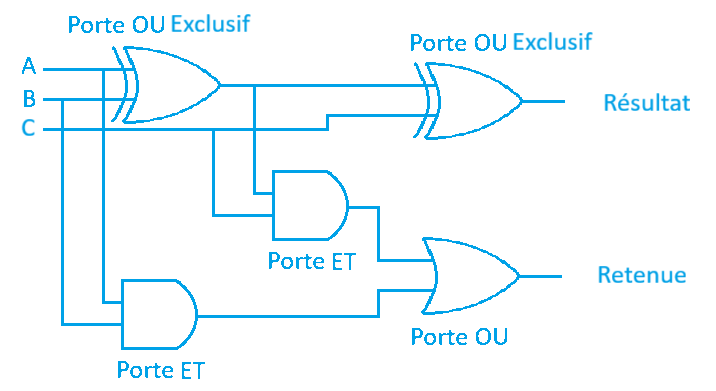
Nous avons doublé la taille de notre « Demi-Additionneur », ce qui nous donne notre circuit « Additionneur » complet. Sa table de vérité est la suivante :

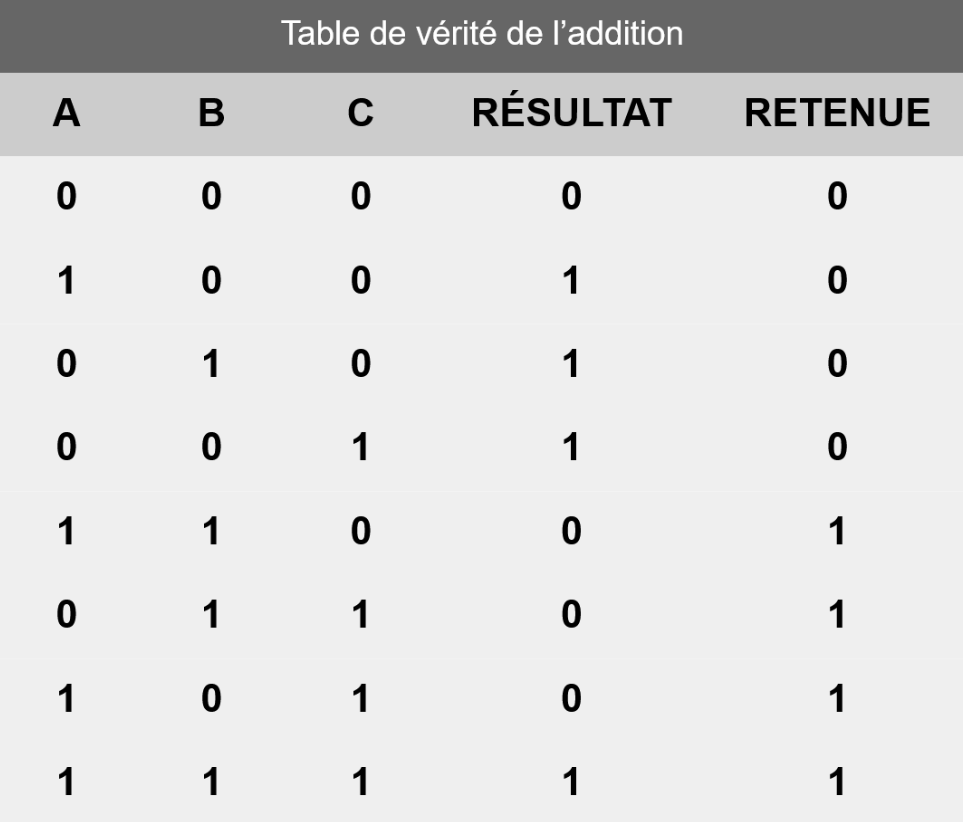
Il est maintenant possible d'en ajouter d'autres à la suite pour faire des opérations de taille (théorique) infinie. Voici par exemple un circuit avec deux additionneurs à la suite :

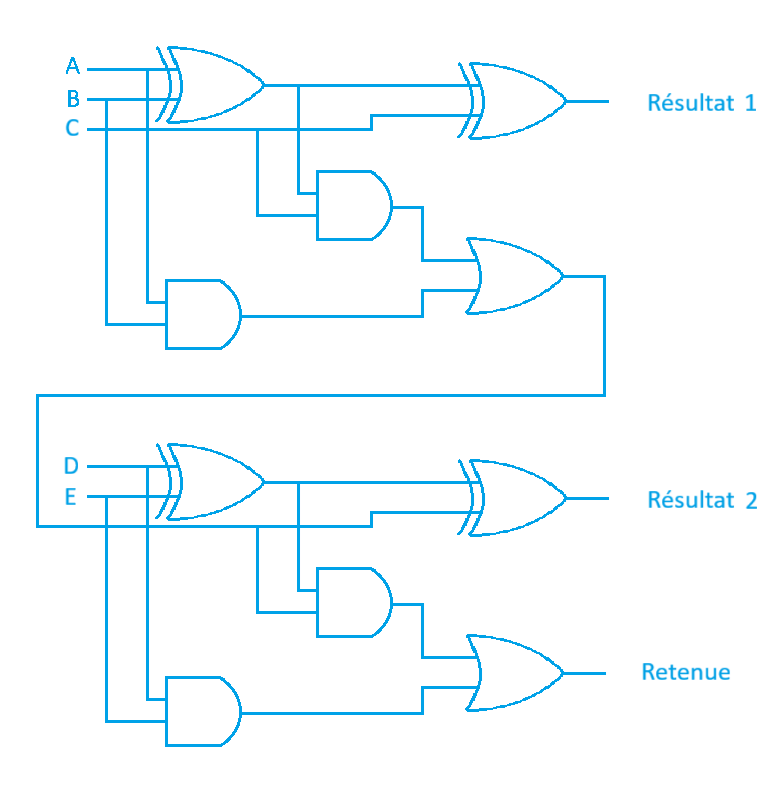
Faisons une pause bien méritée dans notre apprentissage pour réaliser ce que nous venons de comprendre. En partant d'un simple interrupteur (le transistor), nous avons :

- Défini une convention (0 et 1) pour représenter son état.

- Utilisé un système de numération (le binaire) basé sur ces deux états.

- Assemblé des transistors pour créer des portes logiques de base (ET, OU, NON).

- Combiné ces portes pour en créer une plus complexe (XOR).

- Assemblé ces portes d'une manière spécifique pour créer un circuit qui effectue des additions.

In fine, nous avons appris à agencer des morceaux de silicium de manière à "faire des maths". Bien que cet additionneur soit encore très simple, il nécessite, selon sa conception, entre au moins 16 et 20 transistors pour être réalisés. On comprend alors que plus un circuit a de transistors, plus il peut réaliser des opérations complexes. C’est pour cela que le nombre de transistors n’a cessé d’augmenter au fil du temps dans les appareils électroniques qui nous entoure. Cela leur a permis de devenir plus « intelligents ». Ce phénomène est décrit par la loi de Moore. Dans les ordinateurs modernes, les transistors sont concentrés en très grand nombre dans une puce comprenant plusieurs circuits différents, appelé le « processeur ». Ce composant, parfois surnommé le « cerveau » de l’ordinateur, est le contrôleur et calculateur central qui comporte le plus de fonctions différentes et orchestre tout ce qui se passe.